18 - maximum path sum i
By starting at the top of the triangle below and moving to adjacent numbers on the row below, the maximum total from top to bottom is 23.
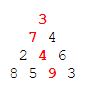
That is, 3 + 7 + 4 + 9 = 23.
Find the maximum total from top to bottom of the triangle below:

NOTE: As there are only 16384 routes, it is possible to solve this problem by trying every route. However, Problem 67, is the same challenge with a triangle containing one-hundred rows; it cannot be solved by brute force, and requires a clever method! ;o)
cozum ile ilgili ip ucu burada
cevap : 1074
Derleme ortami Visual studio community c++
// project euler problem 18
// yasin tasan --> oct 2016
#include "stdafx.h"
int main()
{
unsigned int array[15][15] = {
{ 75, 00, 00, 00, 00, 00, 00, 00, 00, 00, 00, 00, 00, 00, 00 },
{ 95, 64, 00, 00, 00, 00, 00, 00, 00, 00, 00, 00, 00, 00, 00 },
{ 17, 47, 82, 00, 00, 00, 00, 00, 00, 00, 00, 00, 00, 00, 00 },
{ 18, 35, 87, 10, 00, 00, 00, 00, 00, 00, 00, 00, 00, 00, 00 },
{ 20, 04, 82, 47, 65, 00, 00, 00, 00, 00, 00, 00, 00, 00, 00 },
{ 19, 01, 23, 75, 03, 34, 00, 00, 00, 00, 00, 00, 00, 00, 00 },
{ 88, 02, 77, 73, 07, 63, 67, 00, 00, 00, 00, 00, 00, 00, 00 },
{ 99, 65, 04, 28, 06, 16, 70, 92, 00, 00, 00, 00, 00, 00, 00 },
{ 41, 41, 26, 56, 83, 40, 80, 70, 33, 00, 00, 00, 00, 00, 00 },
{ 41, 48, 72, 33, 47, 32, 37, 16, 94, 29, 00, 00, 00, 00, 00 },
{ 53, 71, 44, 65, 25, 43, 91, 52, 97, 51, 14, 00, 00, 00, 00 },
{ 70, 11, 33, 28, 77, 73, 17, 78, 39, 68, 17, 57, 00, 00, 00 },
{ 91, 71, 52, 38, 17, 14, 91, 43, 58, 50, 27, 29, 48, 00, 00 },
{ 63, 66, 04, 68, 89, 53, 67, 30, 73, 16, 69, 87, 40, 31, 00 },
{ 04, 62, 98, 27, 23, 9, 70, 98, 73, 93, 38, 53, 60, 04, 23 },
};
unsigned int var0, var1, n, m, temp[15] = {};
for (m = 14; m > 0; m--)
{
for (n = 0; n < 14; n++)
{
var0 = array[m - 1][n] + array[m][n];
var1 = array[m - 1][n] + array[m][n + 1];
if (var0>var1)
temp[n] = var0;
else
temp[n] = var1;
array[m - 1][n] = temp[n];
}
}
printf("max sum = %d", array[0][0]);
return 0;
}