29 - distinct powers

Consider all integer combinations of ab for 2 ≤ a ≤ 5 and 2 ≤ b ≤ 5:

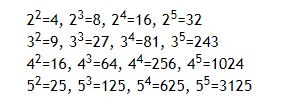
distinct_powers_0

If they are then placed in numerical order, with any repeats removed, we get the following sequence of 15 distinct terms:

4, 8, 9, 16, 25, 27, 32, 64, 81, 125, 243, 256, 625, 1024, 3125

How many distinct terms are in the sequence generated by a^b for 2 ≤ a ≤ 100 and 2 ≤ b ≤ 100?

cevap : 9183

link

Derleme ortami Visual studio community c#

// project euler problem 29
// yasin tasan --> may 2018
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Numerics;
using System.IO;

namespace _29_
{
    class Program
    {
        static void Main(string[] args)
        {
            const int start = 2;
            const int finish = 101;
            const int limit = (finish - start) * (finish - start);
            List<BigInteger> arr = new List<BigInteger>();
            List<BigInteger> arr_ = new List<BigInteger>();
            int i = 0;
            int j = 0;
            int k = 0;
            UInt32 counter = 0;
            UInt32 result = 0;
            StreamWriter sw = new StreamWriter("../../output.txt");

            for (UInt32 a = start; a < finish; a++)
            {
                for (UInt32 b = start; b < finish; b++)
                {
                    arr.Add((BigInteger)Math.Pow(a, b));
                    Console.WriteLine("{0}^{1} = {2}", a, b, arr[i]);
                    sw.WriteLine("{0}^{1} = {2}", a, b, arr[i]);
                    i++;
                }
            }

            Console.WriteLine("");
            sw.WriteLine("");

            arr.Sort();

            // print sorted array
            for (i = 0; i < limit; i++)
            {
                Console.WriteLine("arr[{0}] = {1}", i, arr[i]);
                sw.WriteLine("arr[{0}] = {1}", i, arr[i]);
            }

            Console.WriteLine("");
            sw.WriteLine("");

            //check repeating value
            for (i = 0; i < limit; i++)
            {
                if (i<limit-1)
                {
                    if (arr[i] == arr[i + 1] && arr[i] != 0)
                    {
                        arr_.Add(arr[i]);
                        Console.WriteLine("arr_[{0}] = {1}", k, arr_[k]);
                        sw.WriteLine("arr_[{0}] = {1}", k, arr_[k]);
                        k++;
                        counter++;
                        Console.WriteLine("counter = {0}", counter);
                        sw.WriteLine("counter = {0}", counter);
                    }
                }
            }

            result = limit - counter;
            Console.WriteLine("result = {0}", result);
            sw.WriteLine("result = {0}", result);
            sw.Flush();
            Console.ReadKey();
        }
    }
}